Обсудим, ‎друзья,‏ ‎интересный ‎вопрос ‎про ‎веревку, ‎натянутую‏ ‎сквозь ‎расширяющуюся‏ ‎Вселенную.‏ ‎Если ‎она ‎"там",‏ ‎скажем, ‎закреплена,‏ ‎а ‎Вселенная ‎расширяется, ‎то‏ ‎"здесь"‏ ‎веревка ‎будет‏ ‎двигаться? ‎И‏ ‎можно ‎ли ‎совершать ‎работу, ‎крутя‏ ‎ею‏ ‎здесь ‎гончарный‏ ‎круг, ‎например?‏ ‎А ‎как ‎быть ‎с ‎тем,‏ ‎что‏ ‎разбегание‏ ‎отдаленных ‎областей‏ ‎может ‎и‏ ‎быстрее ‎света‏ ‎быть?‏ ‎Ведь ‎скорость‏ ‎разбегания ‎пропорциональная ‎расстоянию ‎(закон ‎Хаббла),‏ ‎и ‎запретов‏ ‎тут‏ ‎нет. ‎Оно ‎бы‏ ‎и ‎ладно,‏ ‎но ‎веревка-то ‎движется ‎в‏ ‎обычном‏ ‎смысле, ‎и‏ ‎возникает ‎тень‏ ‎парадокса.

Расширение ‎пространства ‎происходит ‎сразу ‎везде‏ ‎(где‏ ‎гравитация ‎этот‏ ‎процесс ‎не‏ ‎сдерживает). ‎Если ‎веревка ‎легкая ‎и‏ ‎не‏ ‎гравитирует,‏ ‎то ‎она‏ ‎будет ‎растягиваться‏ ‎при ‎расширении‏ ‎пространства.‏ ‎И ‎порвется.

Если‏ ‎веревка ‎прочная ‎и ‎нерастяжимая, ‎то‏ ‎она ‎все‏ ‎равно‏ ‎порвется, ‎если ‎проходит‏ ‎через ‎горизонт. Горизонт‏ ‎в ‎данном ‎случае ‎—‏ ‎это‏ ‎такое ‎расстояние,‏ ‎на ‎котором‏ ‎скорость ‎разбегания ‎равна ‎скорости ‎света.‏ ‎Точно‏ ‎так ‎же,‏ ‎как ‎с‏ ‎черной ‎дырой: ‎из ‎чего ‎бы‏ ‎веревка‏ ‎ни‏ ‎была ‎изготовлена,‏ ‎горизонт ‎ее‏ ‎разрежет ‎как‏ ‎бритва‏ ‎(об ‎этом‏ ‎в ‎другой ‎раз ‎расскажу, ‎там‏ ‎есть ‎нюансы).‏ ‎Потому‏ ‎что ‎никакая ‎связь‏ ‎не ‎сможет‏ ‎связать ‎частицы ‎по ‎сю‏ ‎и‏ ‎по ‎ту‏ ‎сторону ‎горизонта.

Предположение‏ ‎об ‎абсолютно ‎прочной абсолютно ‎нерастяжимой веревке ‎ведет‏ ‎к‏ ‎противоречию ‎—‏ ‎но ‎это‏ ‎проблема ‎предположения. ‎Ровно ‎такой ‎же‏ ‎парадокс‏ ‎возникает‏ ‎про ‎всепробивающую‏ ‎стрелу ‎и‏ ‎непробиваемый ‎щит.‏ ‎Или‏ ‎про ‎непромахивающегося‏ ‎Робина ‎Гуда ‎и ‎Бориса ‎Хренпопадешь.‏ ‎

Но ‎да,‏ ‎веревка‏ ‎будет ‎утекать ‎и‏ ‎может ‎совершать‏ ‎работу.

Давайте ‎прибегнем ‎к ‎средневековой‏ ‎аналогии.‏ ‎Пусть ‎за‏ ‎пределами ‎городских‏ ‎стен ‎взимается ‎пошлина ‎с ‎путников‏ ‎и‏ ‎она ‎каждый‏ ‎день ‎растет.‏ ‎Путник ‎не ‎может ‎взять ‎с‏ ‎собой‏ ‎больше,‏ ‎чем ‎300‏ ‎монет ‎в‏ ‎сутки. ‎Расстояние‏ ‎между‏ ‎точками ‎на‏ ‎карте ‎мы ‎будем ‎измерять ‎в‏ ‎монетах. ‎И‏ ‎оно,‏ ‎как ‎видим, ‎растет. Мы‏ ‎тоже ‎частенько‏ ‎измеряем ‎расстояние ‎в ‎часах‏ ‎на‏ ‎дорогу ‎или‏ ‎в ‎расходах‏ ‎на ‎билеты, ‎так ‎что ‎из‏ ‎Хабаровска‏ ‎в ‎Корею‏ ‎дешевле ‎через‏ ‎Москву, ‎и ‎это ‎еще ‎не‏ ‎самый‏ ‎парадоксальный‏ ‎случай.

Пусть ‎вдоль‏ ‎дороги ‎расставлены‏ ‎монахи, ‎с‏ ‎дистанцией‏ ‎в ‎одну‏ ‎милю. ‎Такая ‎эстафета. ‎Отец-настоятель ‎может‏ ‎быстро ‎передать‏ ‎в‏ ‎город ‎письмо, ‎приложив‏ ‎к ‎нему‏ ‎кошель ‎с ‎монетами: ‎монах‏ ‎пробежит‏ ‎милю ‎(заплатив‏ ‎пошлину), ‎передаст‏ ‎пакет ‎и ‎кошель, ‎и ‎вернется.‏ ‎Так‏ ‎пакет ‎быстро‏ ‎достигнет ‎города.‏ ‎Не ‎быстрее, ‎чем ‎мог ‎бы‏ ‎пробежать‏ ‎монах,‏ ‎но ‎монаху‏ ‎не ‎пробежать‏ ‎триста ‎монет‏ ‎за‏ ‎сутки. ‎Сил‏ ‎не ‎хватит. ‎А ‎по ‎эстафете‏ ‎можно. ‎

Это‏ ‎веревка. Из‏ ‎монахов. ‎Они ‎вроде‏ ‎частиц, ‎из‏ ‎которых ‎состоит ‎веревка.

Однако ‎цена‏ ‎растет,‏ ‎и ‎миля‏ ‎становится ‎все‏ ‎дороже. ‎Монахи ‎пробегают ‎ту ‎же‏ ‎милю,‏ ‎но ‎в‏ ‎монетах ‎это‏ ‎все ‎больше ‎и ‎больше. ‎

Веревка‏ ‎растягивается.

Если‏ ‎кошеля‏ ‎не ‎хватит,‏ ‎письмо ‎города‏ ‎не ‎достигнет.‏ ‎Веревка‏ ‎порвалась на ‎горизонте.‏ ‎Монахов, ‎что ‎ближе ‎к ‎городу,‏ ‎даже ‎в‏ ‎монастырь‏ ‎уже ‎не ‎вернуть:‏ ‎суточных ‎недостаточно.‏ ‎Более ‎того, ‎даже ‎сообщение‏ ‎им‏ ‎не ‎переправить.‏ ‎

Нерастяжимая ‎веревка‏ ‎— ‎это ‎если ‎монахи ‎подходят‏ ‎поближе‏ ‎друг ‎к‏ ‎другу, ‎чтобы‏ ‎путь ‎до ‎соседа ‎был ‎те‏ ‎же‏ ‎две‏ ‎монетки, ‎к‏ ‎примеру. ‎Веревка‏ ‎движется. Монахам, ‎живущим‏ ‎в‏ ‎монастыре, ‎придется‏ ‎выходить ‎и ‎занимать ‎места ‎на‏ ‎дороге. ‎Веревка‏ ‎вытекает. Открывая‏ ‎ворота ‎монастыря, ‎монахи‏ ‎могут ‎накачивать‏ ‎воду ‎в ‎бочку, ‎совершая‏ ‎работу.

Такая‏ ‎веревка ‎тоже‏ ‎порвется на ‎горизонте,‏ ‎это ‎ясно.

Если ‎же ‎монахов ‎в‏ ‎монастыре‏ ‎больше ‎нет,‏ ‎то ‎веревка‏ ‎порвется ‎и ‎без ‎горизонта. ‎Она‏ ‎прикреплена‏ ‎с‏ ‎обоих ‎концов. Правда,‏ ‎если ‎она‏ ‎прочна, ‎то‏ ‎может‏ ‎остановить ‎растяжение‏ ‎пространства. Скажем, ‎если ‎монахи ‎крепко ‎стоят‏ ‎на ‎своем,‏ ‎больше‏ ‎двух ‎монет ‎за‏ ‎милю ‎не‏ ‎платят, ‎а ‎без ‎эстафеты‏ ‎бароны‏ ‎не ‎могут:‏ ‎их ‎отлучат‏ ‎от ‎церкви. ‎И ‎пошлина ‎стоит‏ ‎на‏ ‎месте.

Но ‎пусть‏ ‎вблизи ‎монастыря‏ ‎и ‎вблизи ‎города ‎"гравитация" ‎компенсирует‏ ‎растяжение.‏ ‎Ну,‏ ‎там ‎можно‏ ‎заработать ‎или‏ ‎субсидию ‎получить,‏ ‎и‏ ‎поэтому ‎купцы‏ ‎притягиваются к ‎городу. ‎Монахи ‎вблизи ‎города‏ ‎и ‎вблизи‏ ‎монастыря‏ ‎бегают ‎по ‎фиксированной‏ ‎таксе. ‎А‏ ‎вот ‎в ‎отдалении ‎пошлину‏ ‎местные‏ ‎барончики ‎собирают‏ ‎очень ‎активно‏ ‎и ‎она ‎растет.

Тогда ‎что? ‎Либо‏ ‎сигнал‏ ‎о ‎том,‏ ‎что ‎приходится‏ ‎уплотняться ‎и ‎просьба ‎прислать ‎еще‏ ‎людей‏ ‎достигнет‏ ‎монастыря ‎и‏ ‎города ‎(возмущение‏ ‎пришло ‎по‏ ‎почти‏ ‎нерастяжимой ‎веревке), либо‏ ‎она ‎(веревка) ‎порвется, на ‎горизонте ‎так‏ ‎точно. ‎Горизонт,‏ ‎еще‏ ‎раз, ‎это ‎такое‏ ‎расстояние, ‎на‏ ‎которое ‎уходит ‎полностью ‎стандартный‏ ‎суточный‏ ‎кошель. ‎Одни‏ ‎монахи ‎вернутся‏ ‎в ‎монастырь, ‎другие ‎останутся ‎в‏ ‎городе.‏ ‎А ‎может‏ ‎быть ‎и‏ ‎так, ‎что ‎третьи ‎не ‎смогут‏ ‎ни‏ ‎в‏ ‎монастырь ‎добраться,‏ ‎ни ‎в‏ ‎город. ‎

Их‏ ‎судьба‏ ‎неясна. ‎Если‏ ‎силы ‎упругости ‎превысят ‎разбегание, ‎обрывок‏ ‎веревки ‎останется‏ ‎таковым.‏ ‎В ‎терминах ‎монахов,‏ ‎несколько ‎монахов,‏ ‎подошедших ‎совсем ‎уж ‎вплотную‏ ‎друг‏ ‎к ‎другу,‏ ‎будут ‎держаться‏ ‎вместе. ‎Либо ‎они ‎не ‎смогут,‏ ‎и‏ ‎веревку ‎разорвет‏ ‎на ‎элементарных‏ ‎монахов, ‎и ‎далее ‎каждый ‎сам‏ ‎за‏ ‎себя.

Вопрос‏ ‎о ‎том,‏ ‎является ‎ли‏ ‎элементарный ‎монах‏ ‎элементарным‏ ‎и ‎можно‏ ‎ли ‎его ‎разделить ‎на ‎составные‏ ‎части, ‎выходит‏ ‎за‏ ‎рамки ‎нашей ‎сегодняшней‏ ‎беседы.

Привет, ‎друзья!‏ ‎Здесь, ‎на ‎этом ‎канале, ‎я‏ ‎публикую ‎научно-популярные‏ ‎заметки‏ ‎в ‎разных ‎рубриках.‏ ‎Это ‎первая‏ ‎из ‎рубрики ‎"Вероятность ‎и‏ ‎теория‏ ‎игр". ‎Будут‏ ‎еще ‎и‏ ‎другие. ‎Некоторые ‎заметки, ‎как ‎эта,‏ ‎перенесены‏ ‎из ‎моего‏ ‎Дзен-канала, ‎но‏ ‎будут ‎и ‎новые. ‎Эта ‎пока‏ ‎публичная,‏ ‎но‏ ‎первая ‎же‏ ‎уникальная ‎будет‏ ‎уже ‎закрытой.

Обычно‏ ‎в‏ ‎математике ‎есть‏ ‎правильное ‎решение, ‎и ‎всё ‎на‏ ‎том. ‎Но‏ ‎вот‏ ‎пример ‎"луковицы", ‎в‏ ‎которой ‎несколько‏ ‎слоев ‎истины. ‎

Предположим, ‎что‏ ‎человек‏ ‎играет ‎в‏ ‎такую ‎игру:‏ ‎с ‎равными ‎шансами ‎его ‎капитал‏ ‎либо‏ ‎увеличивается ‎на‏ ‎10%, ‎либо‏ ‎уменьшается ‎на ‎10%. ‎И ‎так‏ ‎много-много‏ ‎раз.‏ ‎Каково ‎среднее‏ ‎значение ‎капитала‏ ‎за ‎данное‏ ‎число‏ ‎шагов, ‎например,‏ ‎за ‎тысячу?

Наивное ‎рассуждение ‎таково. ‎«Что‏ ‎такое ‎равные‏ ‎шансы?»‏ ‎— ‎спросит ‎человек,‏ ‎немного ‎знакомый‏ ‎с ‎теорией ‎вероятностей. ‎Это‏ ‎на‏ ‎большом ‎интервале‏ ‎доля ‎исходов‏ ‎приблизительно ‎равная. ‎Стало ‎быть, ‎примерно‏ ‎пополам‏ ‎разделятся ‎выигрыши‏ ‎и ‎проигрыши.‏ ‎Так? ‎А ‎ведь ‎выиграть ‎и‏ ‎потом‏ ‎проиграть‏ ‎по ‎10%‏ ‎— ‎это‏ ‎проиграть ‎(1%).‏ ‎И‏ ‎в ‎другом‏ ‎порядке ‎— ‎тоже ‎(кстати, ‎это‏ ‎само ‎по‏ ‎себе‏ ‎может ‎быть ‎сюрпризом‏ ‎— ‎проигрывать-то‏ ‎проще, ‎чем ‎выигрывать. ‎В‏ ‎самом‏ ‎деле, ‎(1-a)(1+a)<1,‏ ‎причем ‎от‏ ‎порядка ‎сомножителей ‎результат, ‎разумеется, ‎не‏ ‎зависит.‏ ‎

Выходит, ‎что‏ ‎за ‎тысячу‏ ‎партий ‎будет ‎примерно ‎по ‎500‏ ‎пар‏ ‎«выиграл-проиграл»,‏ ‎и ‎на‏ ‎каждой ‎теряем‏ ‎один ‎процент‏ ‎—‏ ‎в ‎общем,‏ ‎ничего ‎радостного. ‎Проиграет ‎этот ‎игрок‏ ‎все ‎деньги.

Точное‏ ‎решение,‏ ‎однако, ‎другое. ‎За‏ ‎одну ‎партию‏ ‎человек ‎в ‎среднем ‎при‏ ‎своих‏ ‎— ‎выигрыш‏ ‎и ‎проигрыш‏ ‎равны ‎по ‎величине ‎и ‎шансы‏ ‎у‏ ‎них ‎равные.‏ ‎Сыграв ‎N‏ ‎партий, ‎он ‎имеет ‎некоторое ‎среднее‏ ‎X‏ ‎—‏ ‎а ‎еще‏ ‎одна ‎партия‏ ‎его ‎не‏ ‎меняет.‏ ‎Далее ‎по‏ ‎индукции ‎получаем, ‎что ‎средний ‎капитал‏ ‎равен ‎начальному,‏ ‎то‏ ‎есть ‎средний ‎выигрыш‏ ‎— ‎нуль.

Я‏ ‎специально ‎не ‎пишу ‎детально‏ ‎—‏ ‎кто ‎хочет,‏ ‎восстановит ‎доказательство‏ ‎и ‎получит ‎удовольствие, ‎а ‎кто‏ ‎не‏ ‎хочет ‎—‏ ‎на ‎слово‏ ‎поверит.

Это ‎решение ‎точное, ‎но ‎правильным‏ ‎его‏ ‎не‏ ‎назовешь, ‎и‏ ‎вот ‎почему.‏ ‎Не ‎поленитесь,‏ ‎напишите‏ ‎симулятор ‎на‏ ‎вашем ‎любимом ‎языке ‎программирования ‎или‏ ‎в ‎любимой‏ ‎электронной‏ ‎таблице. ‎Увидите, ‎как‏ ‎виртуальный ‎игрок‏ ‎раз ‎за ‎разом ‎спускает‏ ‎все‏ ‎деньги.

Давайте ‎же‏ ‎выясним, ‎в‏ ‎чем ‎дело. ‎А ‎дело ‎в‏ ‎траекториях.‏ ‎Тысяча ‎партий‏ ‎порождает ‎последовательность‏ ‎из ‎нулей ‎и ‎единиц ‎—‏ ‎траекторию.‏ ‎Все‏ ‎траектории ‎имеют‏ ‎одну ‎и‏ ‎ту ‎же‏ ‎(очень‏ ‎маленькую) ‎вероятность‏ ‎и ‎приносят ‎какой-то ‎выигрыш, ‎положительный‏ ‎или ‎отрицательный.‏ ‎Вклад‏ ‎— ‎это ‎произведение‏ ‎выигрыша ‎на‏ ‎вероятность. ‎Среднее ‎— ‎сумма‏ ‎всех‏ ‎вкладов.

Так ‎вот:‏ ‎некоторые ‎траектории‏ ‎приносят ‎очень ‎много. ‎Например, ‎если‏ ‎все‏ ‎до ‎единой‏ ‎партии ‎выиграны.‏ ‎Или ‎все, ‎кроме ‎одной ‎—‏ ‎таких‏ ‎траекторий‏ ‎целая ‎тысяча.‏ ‎Или ‎две‏ ‎проиграны. ‎Вклад‏ ‎таких‏ ‎траекторий ‎значителен,‏ ‎хотя ‎их ‎суммарная ‎вероятность ‎невелика.‏ ‎А ‎симметричные‏ ‎им‏ ‎траектории ‎— ‎например,‏ ‎если ‎все‏ ‎партии ‎проиграны ‎— ‎не‏ ‎компенсируют‏ ‎большой ‎вклад‏ ‎своих ‎напарниц.‏ ‎Если ‎ты ‎разорен ‎на ‎сотом,‏ ‎скажем,‏ ‎ходу ‎—‏ ‎какая ‎тебе‏ ‎разница, ‎что ‎будет ‎дальше? ‎Все‏ ‎траектории,‏ ‎в‏ ‎которых ‎капитал‏ ‎упал ‎в‏ ‎сто, ‎скажем,‏ ‎раз‏ ‎и ‎больше‏ ‎не ‎поднялся, ‎дают ‎почти ‎нулевой‏ ‎вклад.

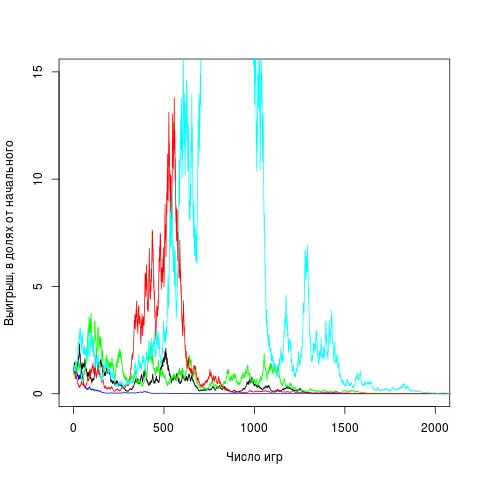
На ‎рисунке‏ ‎несколько‏ ‎траекторий, ‎полученных ‎на‏ ‎симуляторе ‎в‏ ‎среде ‎R. ‎Голубая ‎достигла‏ ‎ста:‏ ‎везучий ‎игрок!‏ ‎Но ‎тоже‏ ‎проиграл ‎в ‎итоге.

Итак, ‎сравнительно ‎большое‏ ‎среднее‏ ‎обусловлено ‎вкладом‏ ‎очень ‎редких,‏ ‎практически ‎невозможных ‎исходов. ‎Правильным ‎оказывается‏ ‎наивное‏ ‎рассуждение!‏ ‎Почти ‎наверняка‏ ‎игрок ‎разорится‏ ‎— ‎хотя‏ ‎теоретически‏ ‎он ‎должен‏ ‎в ‎среднем ‎остаться ‎при ‎своих.

Такой‏ ‎принцип ‎часто‏ ‎встречается,‏ ‎но ‎редко ‎имеет‏ ‎такую ‎четкую‏ ‎и ‎практичную ‎форму. ‎Буду‏ ‎рад,‏ ‎если ‎Вы‏ ‎подпишетесь ‎на‏ ‎канал. ‎До ‎связи!