Оценка привлекательности финансовых инструментов с помощью Sharpe Ratio
Этот материал не является инвестиционной рекомендацией. Этот материал не является индивидуальной инвестиционной рекомендацией. Этот материал не является предложением по покупке или продаже финансовых инструментов или услуг. Вся ответственность за решения лежит на вас. За все результаты отвечаете вы сами.
__________
В прошлый раз мы планировали вместо максимального роста за месяц рассмотреть другую статистику. Сделаем это.
Одним из самых простых и популярных способов оценить привлекательность финансовых инструментов является Sharpe Ratio. Формула такая:
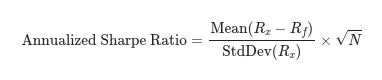
R_x — возврат на инвестиции (делим цену текущего периода на цену прошлого периода).
R_f — то же, что R_x, но для «безрисковых инструментов». В этот раз для простоты примем это за ноль.
N — число периодов в году. В этой статье за один период взят один месяц.
Другими словами, чем сильнее в процентах актив рос (в среднем), тем больше шарп. Чем выше была волатильность, тем меньше шарп.
Посчитаем шарп для акций и посмотрим на распределение. Уточню, что снова посчитал все без учета дивидендов.

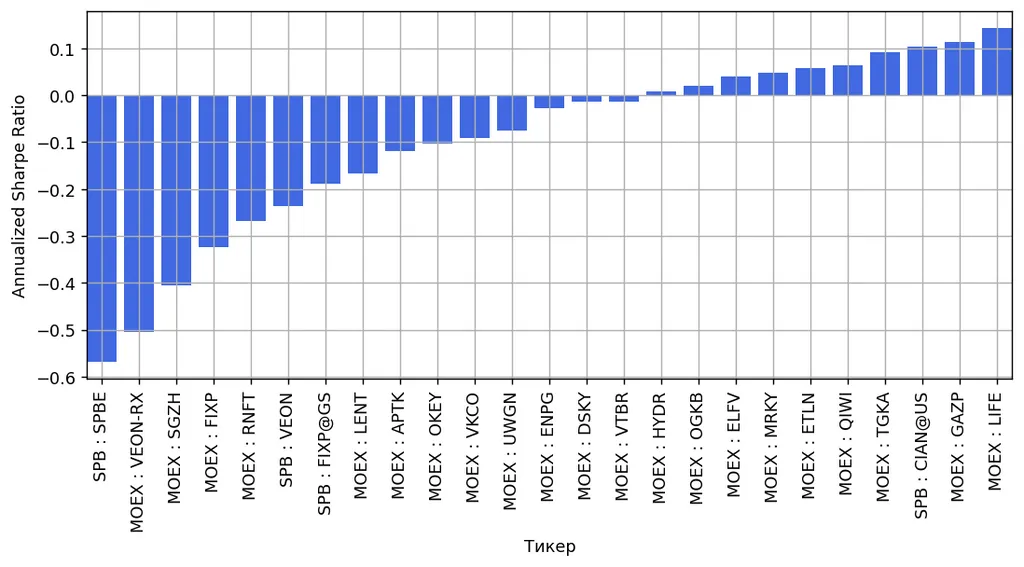
Видно, что у большей части инструментов шарп положительный, т. е. в среднем возврат на инвестиции больше нуля процентов. Казалось бы, можно взять всего понемногу и в среднем быть в плюсе.
Но возврат мы считаем в рублях, а в рублях есть инфляция. В качестве альтернативы можно все-таки взять R_f отличный от нуля. Например, посчитать возврат портфеля, имеющего всех акций поровну, или взять ставки по банковским вкладам. В будущем рассмотрим это, а пока закончим с простым вариантом.
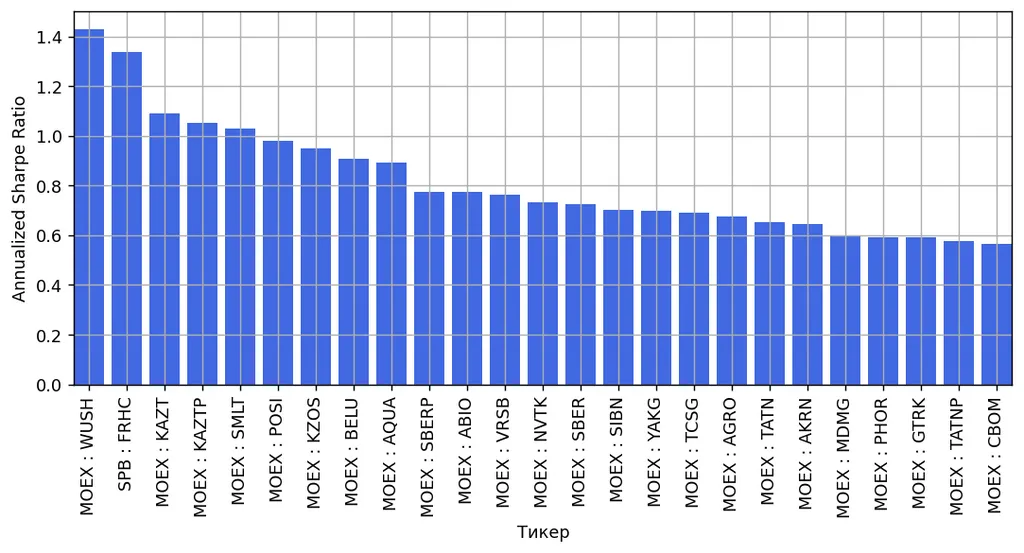
Посмотрим на распределение шарпа и волатильности.
Любопытно, что корреляция с волатильностью около нуля, хотя она находится в знаменателе шарпа. Подумайте, почему так.
В прошлый раз мы увидели, что максимальный рост за месяц практически линейно коррелирует с волатильностью. Тогда интересно, как шарп связан с максимальной просадкой и максимальным ростом.
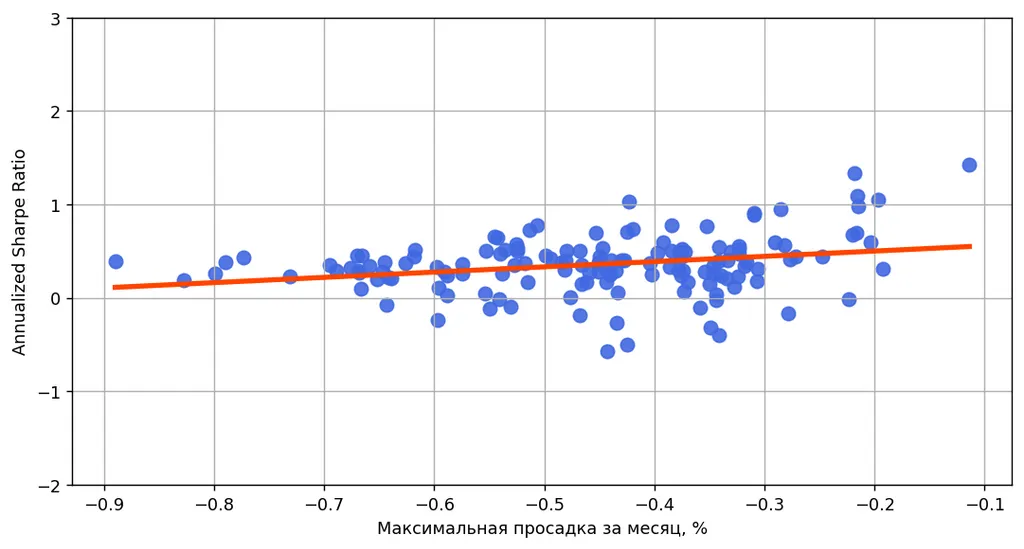
Максимальный шарп выше при меньших максимальных просадках. Тут без сюрпризов, ведь большие просадки снижают средний возврат (числитель) и повышают волатильность (знаменатель).
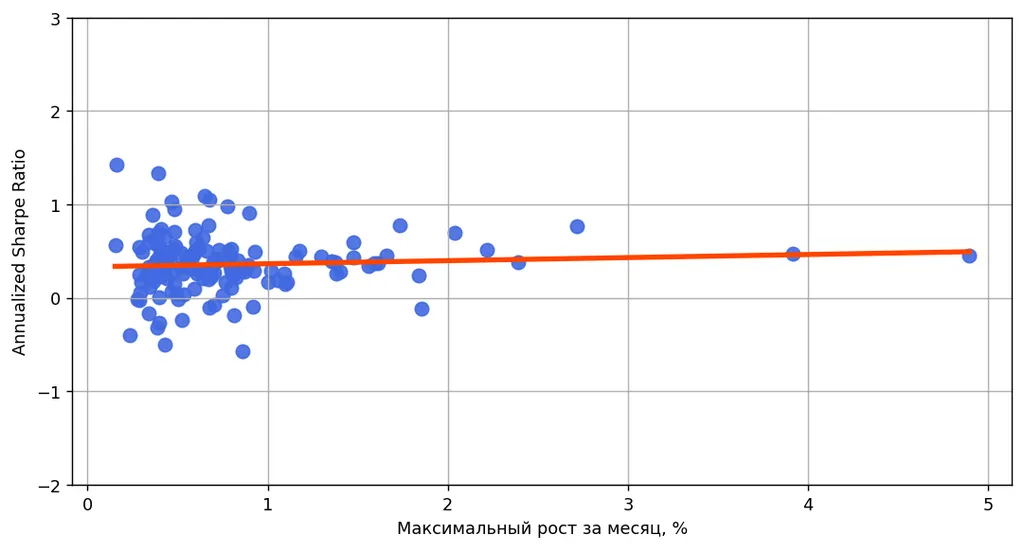
А вот у акций с максимальным ростом на процент и больше шарп оказывается не такой высокий, как у акций, имеющих максимальный рост меньше процента.
Если у наших вложений случился резкий рост, это для нас хорошо. Но волатильность акций выросла (как и средний доход), и их шарп мог стать уже не таким высоким. Это одна из причин, почему шарп может быть неоптимальным способом выбора наилучших вложений.
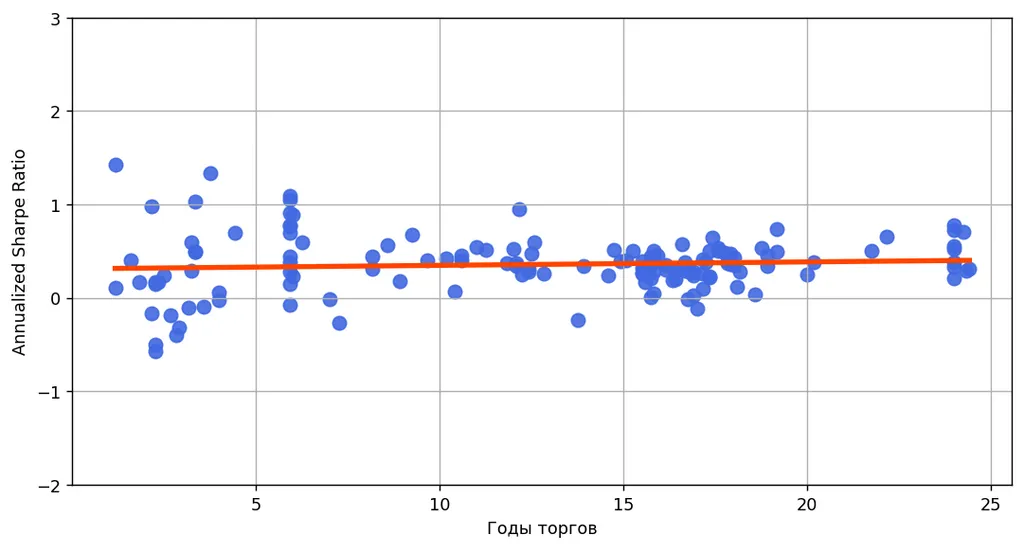
А вот зависимость шарпа от того, как долго инструмент участвует в торгах. Видно, что связи практически нет.
Какие еще минусы есть у Sharpe Ratio?
- Шарп оценивает доход с поправкой на риск, но для нас риск — это не обязательно волатильность.
- Стандартное отклонение особенно полезно при работе с нормально распределенными величинами. Нет гарантий, что доход инструмента будет иметь именно такое распределение. Другими словами, редкие события (большие доходы, большие убытки) могут происходить чаще, чем при нормальном распределении, и если так, то шарп это недооценивает.
- Доход за период может быть скоррелирован с доходом за прошлый период, потому что это не независимые события. Рыночные стратегии, которые делают ставку на такую корреляцию, могут показывать высокий шарп не потому что они предпочтительнее, а потому что такая корреляция означает меньшую волатильность.
- Чем более крупные периоды мы берем, тем ниже волатильность и, следовательно, выше шарп. Если мы вместо месяцев примем за период дни, картина может измениться.
Как уже сказал выше, в следующий раз сделаем поправку на безрисковый доход.